Research

My mathematical research is in the general area of optimisation and variational analysis, with some geometric measure theory, everything motivated by inverse imaging and machine learning applications. Specifically, I develop high-performance numerical methods for the solution mathematical models for such problems, and try to understand the solutions of said models; whether those models can be trusted.

Below are some example topics. Further can be found in my list of publications.

Optimisation in spaces of measures

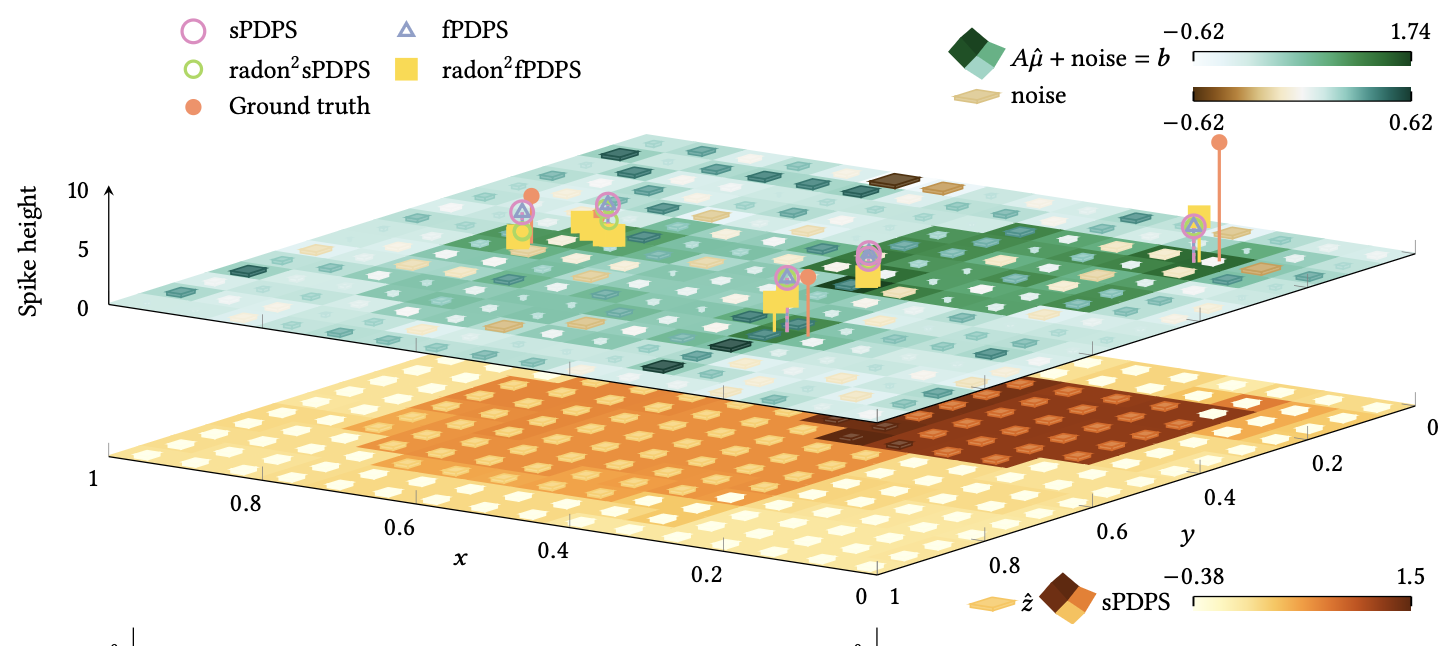
How can we locate point sources, such as stars in the sky or biomarkers in cells, from indirect measurement data? How can we even model the problem, when we do not know their number? We pose it as an optimisation problem in a space of measures!

But how can then solve that problem numerically, and fast?

• Valkonen, Point source localisation with unbalanced optimal transport (2025).

  [ abstract | pdf | arXiv | codes ]

  Replacing the quadratic proximal penalty familiar from Hilbert spaces by an unbalanced optimal transport distance, we develop forward-backward type optimisation methods in spaces of Radon measures. We avoid the actual computation of the optimal transport distances through the use transport three-plans and the rough concept of transport subdifferentials. The resulting algorithm has a step similar to the sliding heuristics previously introduced for conditional gradient methods, however, now non-heuristically derived from the geometry of the space. We demonstrate the improved numerical performance of the approach.

  submitted
• Valkonen, Proximal methods for point source localisation (2022).

  [ abstract | pdf | arXiv | codes ]

  Point source localisation is generally modelled as a Lasso-type problem on measures. However, optimisation methods in non-Hilbert spaces, such as the space of Radon measures, are much less developed than in Hilbert spaces. Most numerical algorithms for point source localisation are based on the Frank–Wolfe conditional gradient method, for which ad hoc convergence theory is developed. We develop extensions of proximal-type methods to spaces of measures. This includes forward-backward splitting, its inertial version, and primal-dual proximal splitting. Their convergence proofs follow standard patterns. We demonstrate their numerical efficacy.

  Journal of Nonsmooth Analysis and Optimization 4 (2023), 10433, doi:10.46298/jnsao-2023-10433
• Valkonen, Proximal methods for point source localisation: the implementation (2022–2025).
  [ project page | zenodo ]
  doi:10.5281/zenodo.14884773

Optimisation on non-Riemannian manifolds

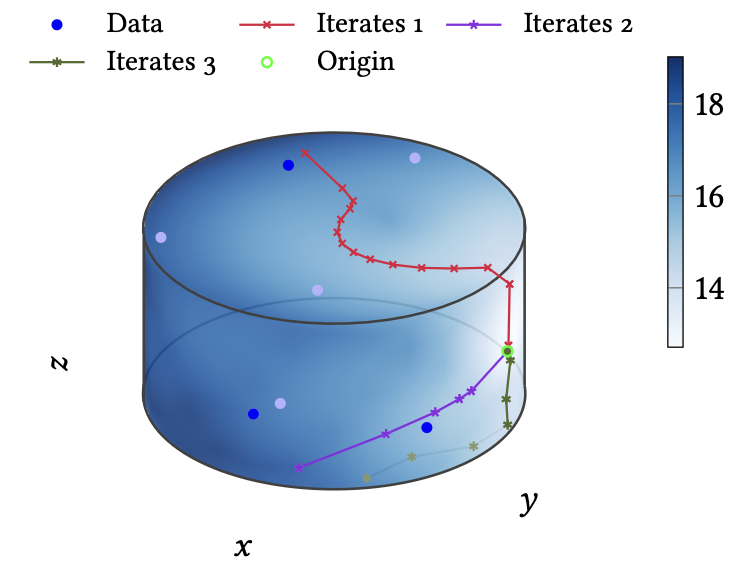
How to find optimal solutions to optimisation problems on surfaces that may have sharp kinks?

• von Koch and Valkonen, Forward-backward splitting in bilaterally bounded Alexandrov spaces (2025).

  [ abstract | pdf | arXiv | codes ]

  With the goal of solving optimisation problems on non-Riemannian manifolds, such as geometrical surfaces with sharp edges, we develop and prove the convergence of a forward-backward method in Alexandrov spaces with curvature bounded both from above and from below. This bilateral boundedness is crucial for the availability of both the gradient and proximal steps, instead of just one or the other. We numerically demonstrate the behaviour of the proposed method on simple geometrical surfaces in $ℝ^3$

  .

  submitted
• Valkonen and von Koch, Non-Riemannian optimisation (2025).
  doi:10.5281/zenodo.15102168, software on Zenodo

High-performance bilevel optimisation methods

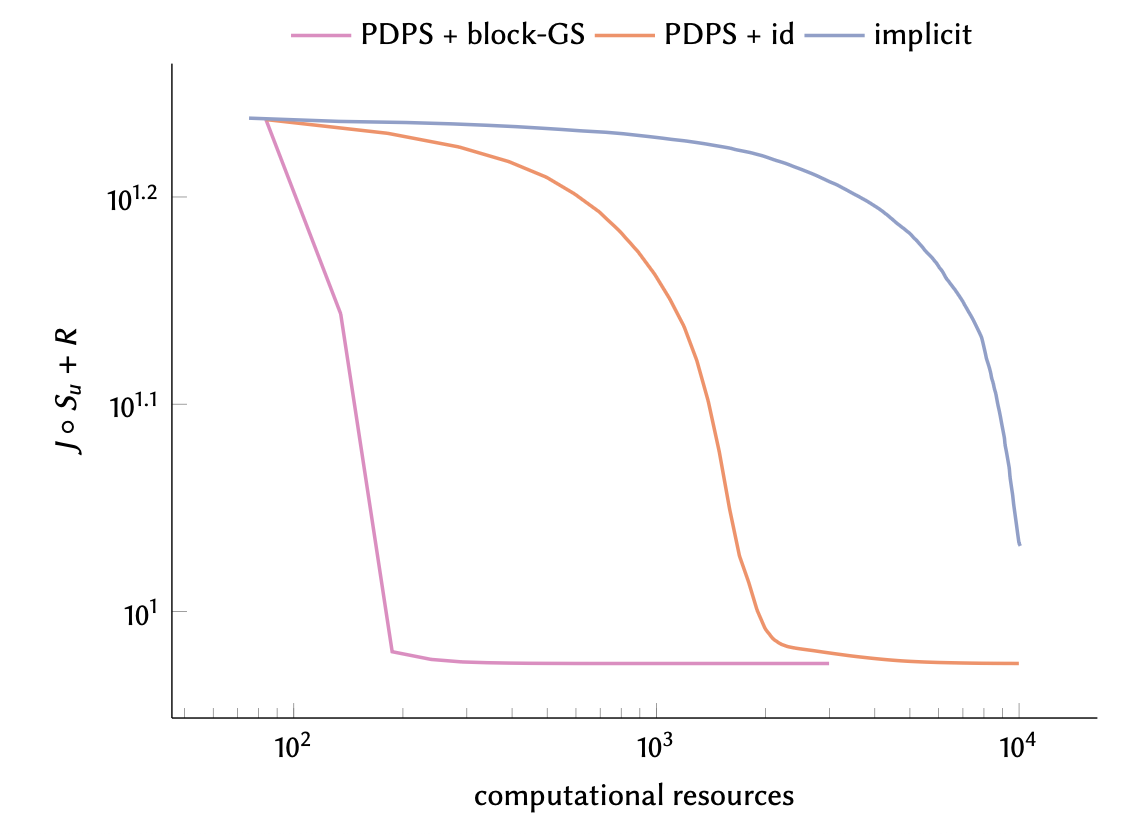
Many learning problems and experimental design problems involve bilevel optimisation: an outer optimisation problem that tries to find the best possible parameters for an inner problem. The latter can be, for example, an image reconstruction problem or a neural network training problem.

How can we solve such problems, and fast?

• Dizon and Valkonen, Differential estimates for fast first-order multilevel nonconvex optimisation (2024).

  [ abstract | pdf | arXiv ]

  With a view on bilevel and PDE-constrained optimisation, we develop iterative estimates $\tilde F'(x^k)$

  of $F'(x^k)$

  for compositions $F := J \circ S$

  , where $S$

  is the solution mapping of the inner optimisation problem or PDE. The idea is to form a single-loop method by interweaving updates of the iterate $x^k$

  by an outer optimisation method, with updates of the estimate by single steps of standard optimisation methods and linear system solvers. When the inner methods satisfy simple tracking inequalities, the differential estimates can almost directly be employed in standard convergence proofs for general forward-backward type methods. We adapt those proofs to a general inexact setting in normed spaces, that, besides our differential estimates, also covers mismatched adjoints and unreachable optimality conditions in measure spaces. As a side product of these efforts, we provide improved convergence results for nonconvex Primal-Dual Proximal Splitting (PDPS).

  submitted
• Suonperä and Valkonen, Single-loop methods for bilevel parameter learning in inverse imaging (2024).

  [ abstract | pdf | arXiv | codes ]

  Bilevel optimisation is used in inverse problems for hyperparameter learning and experimental design. For instance, it can be used to find optimal regularisation parameters and forward operators, based on a set of training pairs. However, computationally, the process is costly. To reduce this cost, recently in bilevel optimisation research, especially as applied to machine learning, so-called single-loop approaches have been introduced. On each step of an outer optimisation method, such methods only take a single gradient descent step towards the solution of the inner problem. In this paper, we flexibilise the inner algorithm, to allow for methods more applicable to difficult inverse problems with nonsmooth regularisation, including primal-dual proximal splitting (PDPS). Moreover, as we have recently shown, significant performance improvements can be obtained in PDE-constrained optimisation by interweaving the steps of conventional iterative solvers (Jacobi, Gauss–Seidel, conjugate gradients) for both the PDE and its adjoint, with the steps of the optimisation method. In this paper we demonstrate how the adjoint equation in bilevel problems can also benefit from such interweaving with conventional linear system solvers. We demonstrate the performance of our proposed methods on learning the deconvolution kernel for image deblurring, and the subsampling operator for magnetic resonance imaging (MRI).

  submitted
• Suonperä and Valkonen, Linearly convergent bilevel optimization with single-step inner methods (2022).

  [ abstract | pdf | arXiv | codes ]

  We propose a new approach to solving bilevel optimization problems, intermediate between solving full-system optimality conditions with a Newton-type approach, and treating the inner problem as an implicit function. The overall idea is to solve the full-system optimality conditions, but to precondition them to alternate between taking steps of simple conventional methods for the inner problem, the adjoint equation, and the outer problem. While the inner objective has to be smooth, the outer objective may be nonsmooth subject to a prox-contractivity condition. We prove linear convergence of the approach for combinations of gradient descent and forward-backward splitting with exact and inexact solution of the adjoint equation. We demonstrate good performance on learning the regularization parameter for anisotropic total variation image denoising, and the convolution kernel for image deconvolution.

  Computational Optimization and Applications 87 (2024), 571–610, doi:10.1007/s10589-023-00527-7

High-performance first-order optimisation methods for inverse problems, static and dynamic

Inverse imaging problems involve the recontruction of a physical field (that we see on the computer screen as an image), such as a conductivity field in electrical impedance tomography (EIT), or water concentration in magnetic resonance imaging (MRI), from indirect measurements. Such problems are ill-posed, and need to be “regularised” with our prior conceptions of a good solutions. This often results in a nonsmooth optimisation problem: the objective function is non-differentiable. Classical optimisation methods are therefore not applicable.

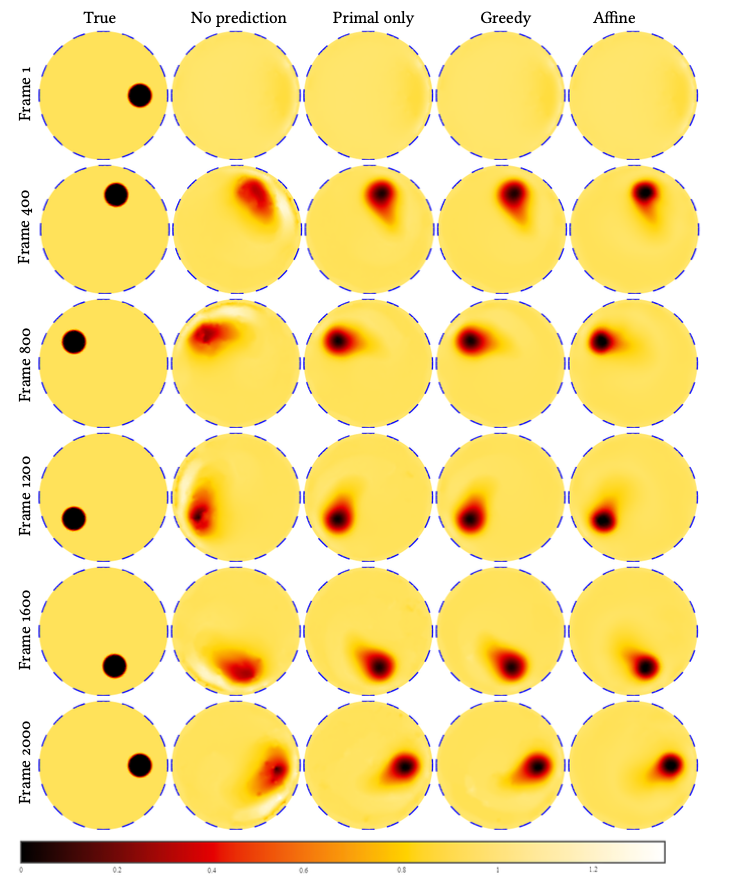
So how can we then solve such problems, and fast? How can we make the methods real-time, for imaging, e.g., rapidly flowing fluids?

• Dizon, Jauhiainen and Valkonen, Online optimisation for dynamic electrical impedance tomography (2024).

  [ abstract | pdf | arXiv | codes ]

  Online optimisation studies the convergence of optimisation methods as the data embedded in the problem changes. Based on this idea, we propose a primal dual online method for nonlinear time-discrete inverse problems. We analyse the method through regret theory and demonstrate its performance in real-time monitoring of moving bodies in a fluid with Electrical Impedance Tomography (EIT). To do so, we also prove the second-order differentiability of the Complete Electrode Model (CEM) solution operator on $L^\infty$

  .

  Inverse Problems 41 (2025), 055005, doi:10.1088/1361-6420/adcb66
• Guerra and Valkonen, Multigrid methods for total variation (2024).

  [ abstract | pdf | arXiv | codes ]

  Based on a nonsmooth coherence condition, we construct and prove the convergence of a forward-backward splitting method that alternates between steps on a fine and a coarse grid. Our focus is an total variation regularised inverse imaging problems, specifically, their dual problems, for which we develop in detail the relevant coarse-grid problems. We demonstrate the performance of our method on total variation denoising and magnetic resonance imaging.

  Scale Space and Variational Methods in Computer Vision, SSVM 2025, editors: Bubba, Gaburro, Gazzola, Papafitsoros, Pereyra and Schönlieb, Lecture Notes in Computer Science, doi:10.1007/978-3-031-92369-2_1 (2025), 3–16
• Dizon and Valkonen, Differential estimates for fast first-order multilevel nonconvex optimisation (2024).

  [ abstract | pdf | arXiv ]

  With a view on bilevel and PDE-constrained optimisation, we develop iterative estimates $\tilde F'(x^k)$

  of $F'(x^k)$

  for compositions $F := J \circ S$

  , where $S$

  is the solution mapping of the inner optimisation problem or PDE. The idea is to form a single-loop method by interweaving updates of the iterate $x^k$

  by an outer optimisation method, with updates of the estimate by single steps of standard optimisation methods and linear system solvers. When the inner methods satisfy simple tracking inequalities, the differential estimates can almost directly be employed in standard convergence proofs for general forward-backward type methods. We adapt those proofs to a general inexact setting in normed spaces, that, besides our differential estimates, also covers mismatched adjoints and unreachable optimality conditions in measure spaces. As a side product of these efforts, we provide improved convergence results for nonconvex Primal-Dual Proximal Splitting (PDPS).

  submitted
• Dizon, Jauhiainen and Valkonen, Prediction techniques for dynamic imaging with online primal-dual methods (2024).

  [ abstract | pdf | arXiv | codes ]

  Online optimisation facilitates the solution of dynamic inverse problems, such as image stabilisation, fluid flow monitoring, and dynamic medical imaging. In this paper, we improve upon previous work on predictive online primal-dual methods on two fronts. Firstly, we provide a more concise analysis that symmetrises previously unsymmetric regret bounds, and relaxes previous restrictive conditions on the dual predictor. Secondly, based on the latter, we develop several improved dual predictors. We numerically demonstrate their efficacy in image stabilisation and dynamic positron emission tomography.

  Journal of Mathematical Imaging and Vision (2024), doi:10.1007/s10851-024-01214-w
• Jensen and Valkonen, A nonsmooth primal-dual method with interwoven PDE constraint solver (2022).

  [ abstract | pdf | arXiv | codes ]

  We introduce an efficient first-order primal-dual method for the solution of nonsmooth PDE-constrained optimization problems. We achieve this efficiency through not solving the PDE or its linearisation on each iteration of the optimization method. Instead, we run the method interwoven with a simple conventional linear system solver (Jacobi, Gauss–Seidel, conjugate gradients), always taking only one step of the linear system solver for each step of the optimization method. The control parameter is updated on each iteration as determined by the optimization method. We prove linear convergence under a second-order growth condition, and numerically demonstrate the performance on a variety of PDEs related to inverse problems involving boundary measurements.

  Computational Optimization and Applications 89 (2024), 115–149, doi:10.1007/s10589-024-00587-3
• Valkonen, A primal-dual hybrid gradient method for non-linear operators with applications to MRI (2014).

  [ abstract | pdf | arXiv ]

  We study the solution of minimax problems $\min_x \max_y G(x) + \langle K(x), y \rangle - F^*(y)$

  in finite-dimensional Hilbert spaces. The functionals $G$

  and $F^*$

  we assume to be convex, but the operator $K$

  we allow to be non-linear. We formulate a natural extension of the modified primal-dual hybrid gradient method (PDHGM), originally for linear $K$

  , due to Chambolle and Pock. We prove the local convergence of the method, provided various technical conditions are satisfied. These include in particular the Aubin property of the inverse of a monotone operator at the solution. Of particular interest to us is the case arising from Tikhonov type regularisation of inverse problems with non-linear forward operators. Mainly we are interested in total variation and second-order total generalised variation priors. For such problems, we show that our general local convergence result holds when the noise level of the data $f$

  is low, and the regularisation parameter $\alpha$

  is correspondingly small. We verify the numerical performance of the method by applying it to problems from magnetic resonance imaging (MRI) in chemical engineering and medicine. The specific applications are in diffusion tensor imaging (DTI) and MR velocity imaging. These numerical studies show very promising performance.

  Inverse Problems 30 (2014), 055012, doi:10.1088/0266-5611/30/5/055012

Analysis of inverse imaging problems; geometric measure theory

What can we, a priori, before solving the problem, say about the solutions to the above inverse imaging problems? In particular, when we pose the problem in the space of functions of bounded variation (BV), where we can rigorously talk about objects boundaries, can we say that the reconstruction models preserve the boundaries, and do not introduce new artefacts?

• Valkonen, The jump set under geometric regularisation. Part 1: Basic technique and first-order denoising (2015).

  [ abstract | pdf | arXiv ]

  Let $u \in \mbox{BV}(\Omega)$

  solve the total variation denoising problem with $L^2$

  -squared fidelity and data $f$

  . Caselles et al. [Multiscale Model. Simul. 6 (2008), 879–894] have shown the containment $\mathcal{H}^{m-1}(J_u \setminus J_f)=0$

  of the jump set $J_u$

  of $u$

  in that of $f$

  . Their proof unfortunately depends heavily on the co-area formula, as do many results in this area, and as such is not directly extensible to higher-order, curvature-based, and other advanced geometric regularisers, such as total generalised variation (TGV) and Euler's elastica. These have received increased attention in recent times due to their better practical regularisation properties compared to conventional total variation or wavelets. We prove analogous jump set containment properties for a general class of regularisers. We do this with novel Lipschitz transformation techniques, and do not require the co-area formula. In the present Part 1 we demonstrate the general technique on first-order regularisers, while in Part 2 we will extend it to higher-order regularisers. In particular, we concentrate in this part on TV and, as a novelty, Huber-regularised TV. We also demonstrate that the technique would apply to non-convex TV models as well as the Perona-Malik anisotropic diffusion, if these approaches were well-posed to begin with.

  SIAM Journal on Mathematical Analysis 47 (2015), 2587–2629, doi:10.1137/140976248
• Valkonen, The jump set under geometric regularisation. Part 2: Higher-order approaches (2017).

  [ abstract | pdf | arXiv ]

  In Part 1, we developed a new technique based on Lipschitz pushforwards for proving the jump set containment property $\mathcal{H}^{m-1}(J_u \setminus J_f)=0$

  of solutions $u$

  to total variation denoising. We demonstrated that the technique also applies to Huber-regularised TV. Now, in this Part 2, we extend the technique to higher-order regularisers. We are not quite able to prove the property for total generalised variation (TGV) based on the symmetrised gradient for the second-order term. We show that the property holds under three conditions: First, the solution $u$

  is locally bounded. Second, the second-order variable is of locally bounded variation, $w \in \mbox{BV}_{\text{loc}}(\Omega; R^m)$

  , instead of just bounded deformation, $w \in \mbox{BD}(\Omega)$

  . Third, $w$

  does not jump on $J_u$

  parallel to it. The second condition can be achieved for non-symmetric TGV. Both the second and third condition can be achieved if we change the Radon (or $L^1$

  ) norm of the symmetrised gradient $Ew$

  into an $L^p$

  norm, $p>1$

  , in which case Korn's inequality holds. On the positive side, we verify the jump set containment property for second-order infimal convolution TV (ICTV) in dimension $m=2$

  . We also study the limiting behaviour of the singular part of $D u$

  , as the second parameter of $\mbox{TGV}^2$

  goes to zero. Unsurprisingly, it vanishes, but in numerical discretisations the situation looks quite different. Finally, our work additionally includes a result on TGV-strict approximation in $\mbox{BV}(\Omega)$

  .

  Journal of Mathematical Analysis and Applications 453 (2017), 1044–1085, doi:10.1016/j.jmaa.2017.04.037

Set-valued analysis

The analysis of nonsmooth optimisation problems, methods, and inverse problems, often benefits from higher-order “differentiation” of an already set-valued first-order “subdifferential”. In this world, calculus rules and concepts of regularity, such as smoothness, can become very complicated, so how do we make sense of it all?

• Clason and Valkonen, Introduction to Nonsmooth Analysis and Optimization (2024).

  [ abstract | pdf | arXiv | codes ]

  This book aims to give an introduction to generalized derivative concepts useful in deriving necessary optimality conditions and numerical algorithms for infinite-dimensional nondifferentiable optimization problems that arise in inverse problems, imaging, and PDE-constrained optimization. They cover convex subdifferentials, Fenchel duality, monotone operators and resolvents, Moreau–Yosida regularization as well as Clarke and (briefly) limiting subdifferentials. Both first-order (proximal point and splitting) methods and second-order (semismooth Newton) methods are treated. In addition, differentiation of set-valued mapping is discussed and used for deriving second-order optimality conditions for as well as Lipschitz stability properties of minimizers. Applications to inverse problems and optimal control of partial differential equations illustrate the derived results and algorithms. The required background from functional analysis and calculus of variations is also briefly summarized.

  textbook, submitted
• Valkonen, Regularisation, optimisation, subregularity (2020).

  [ abstract | pdf | arXiv | codes ]

  Regularisation theory in Banach spaces, and non–norm-squared regularisation even in finite dimensions, generally relies upon Bregman divergences to replace norm convergence. This is comparable to the extension of first-order optimisation methods to Banach spaces. Bregman divergences can, however, be somewhat suboptimal in terms of descriptiveness. Using the concept of (strong) metric subregularity, previously used to prove the fast local convergence of optimisation methods, we show norm convergence in Banach spaces and for non–norm-squared regularisation. For problems such as total variation regularised image reconstruction, the metric subregularity reduces to a geometric condition on the ground truth: flat areas in the ground truth have to compensate for the kernel of the forward operator. Our approach to proving such regularisation results is based on optimisation formulations of inverse problems. As a side result of the regularisation theory that we develop, we provide regularisation complexity results for optimisation methods: how many steps $N_\delta$

  of the algorithm do we have to take for the approximate solutions to converge as the corruption level $\delta \searrow 0$

  ?

  Inverse Problems 37 (2021), 045010, doi:10.1088/1361-6420/abe4aa
• Valkonen, Preconditioned proximal point methods and notions of partial subregularity (2017).

  [ abstract | pdf | arXiv | link ]

  Based on the needs of convergence proofs of preconditioned proximal point methods, we introduce notions of partial strong submonotonicity and partial (metric) subregularity of set-valued maps. We study relationships between these two concepts, neither of which is generally weaker or stronger than the other one. For our algorithmic purposes, the novel submonotonicity turns out to be easier to employ than more conventional error bounds obtained from subregularity. Using strong submonotonicity, we demonstrate the linear convergence of the Primal-Dual Proximal splitting method to some strictly complementary solutions of example problems from image processing and data science. This is without the conventional assumption that all the objective functions of the involved saddle point problem are strongly convex.

  Journal of Convex Analysis 28 (2021), 251–278
• Clason and Valkonen, Stability of saddle points via explicit coderivatives of pointwise subdifferentials (2017).

  [ abstract | pdf | arXiv ]

  We derive stability criteria for saddle points of a class of nonsmooth optimization problems in Hilbert spaces arising in PDE-constrained optimization, using metric regularity of infinite-dimensional set-valued mappings. A main ingredient is an explicit pointwise characterization of the regular coderivative of the subdifferential of convex integral functionals. This is applied to several stability properties for parameter identification problems for an elliptic partial differential equation with non-differentiable data fitting terms.

  Set-valued and Variational Analysis 25 (2017), 69–112, doi:10.1007/s11228-016-0366-7